Welcome to Illuminating Science, a website dedicated to helping students gain a better conceptual foundation of modern physics. We believe that effective learning happens when abstract concepts are brought to life—so we place a strong emphasis on thoughtfully designed illustrations, visual aids, and intuitive explanations that make modern physics understandable and inspiring.

Our focus is on understanding natural structures embedded in the laws of physics, expressed in the conserved quantities of universal constants, and revealed using tools such as natural units and dimensional analysis. These concepts provide a conceptual foundation that accompanies the mathematics.
Resources for physics educators
This website is designed for physics educators who want to help their students understand the foundational ideas of modern physics. All of the materials here—descriptions, diagrams, and examples—are free to download and use in the classroom. While most of the materials are in the public domain, a few images have been adapted from published journal articles and are presented under the Creative Commons Attribution 4.0 International License. Images that require attribution are noted in the captions.
Teacher’s guide
The following overview is a brief introduction to universal constants, natural units, and dimensional analysis. Additional details can be found in the article Understanding the natural units and their hidden role in the laws of physics (Eur. J. Phys. 45 015805, 2024) and other published works on these topics.
Natural units
It is generally understood that SI units conceal a natural structure that emerges when we set universal constants equal to 1.

We call these “natural units” because they give proportionally meaningful results. For example:
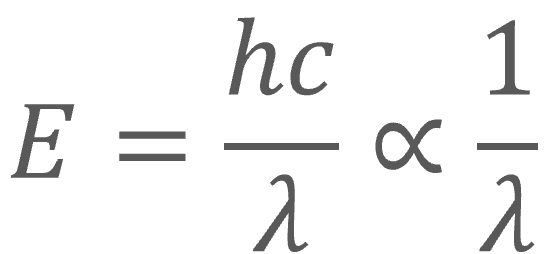
While this is a step in the right direction, there is more that we can learn about natural correlations using another set of natural units called “Planck units.”
Universal constants
The relationship between universal constants and Planck units is often misunderstood. While the values of Planck units can be derived from compound-dimensional universal constants, Planck units give a single value per unit dimension. Universal constants contain discrete Planck units in their unit dimensions.
The 2022 CODATA extensive listing of Fundamental Universal Constants specifies this dimensional structure for the Planck constant and the Speed of Light, while the structure also holds for other universal constants.
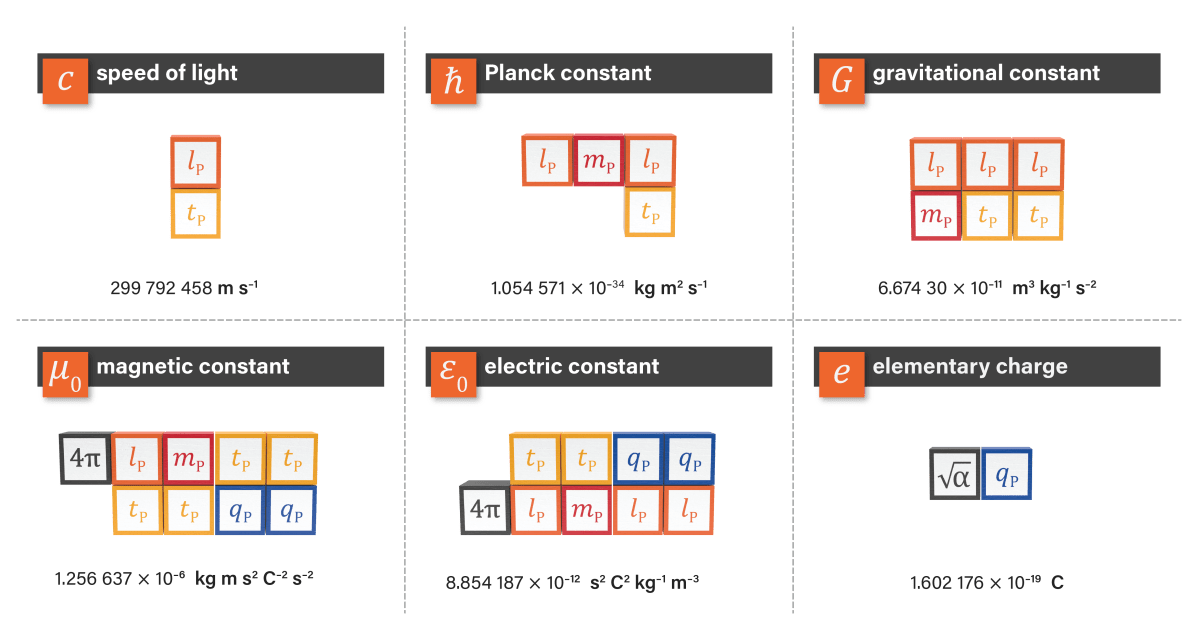
What are Planck Units?
Planck units are natural units of length, mass, time, and electric charge:




Base Planck units can be combined into compound dimensional units.

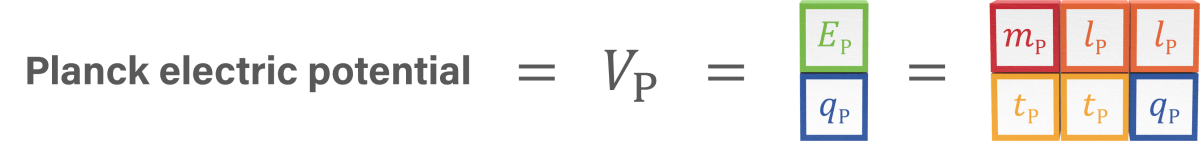
Natural unit formulas
Restating universal constants in Planck units provides deeper insight into the dimensional structure of equations and shows why dimensional analysis works. For example, we can restate the photon energy formula in Planck units

Natural unit formulas illustrate two important characteristics of natural phenomena—correlations in their physical attributes and dynamics, and conservation of quantities that are equivalent to universal constants.

Correlation: Photon wavelength and energy are correlated at the Planck scale. This means that a Planck length photon carries Planck energy. As wavelength increases, energy decreases by an amount equal to the inverse number of length units. In other words, a photon with a wavelength of 100 Planck lengths has 1/100 Planck energy, etc.

Conservation: The inverse proportionality between wavelength and energy conserves the product of Planck length and Planck energy, which is equal to the product of Planck’s constant and the speed of light.

Correlation and conservation are not unique to photon properties; they are found everywhere universal constants appear including equations for gravitational and electromagnetic phenomena. For example, restating the electrostatic force in Planck units shows the conservation of the electric constant.
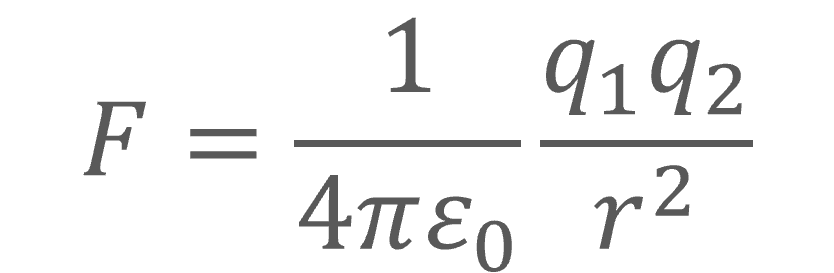
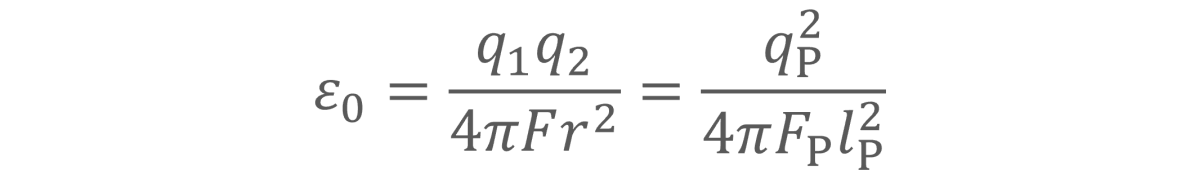
Correlation: Electrostatic force

Conservation: Electric constant

The colored block illustrations are a simple and engaging way for teachers to present dimensional analysis in a way that emphasizes hidden correlations and conservations. The conservation block diagram emphasizes how quantities in each unit dimension change as the phenomenon changes in scale, while correlation block diagrams emphasize correlations of non-dimensional quantities shown in the same color to represent the dimension.
Illustrations showing the conservation of the Planck constant, speed of light, gravitational constant, electric constant, and magnetic constant are available to view and download on the Natural units page and the download page.
Multi-constant phenomena
Combinations of universal constants are sometimes required to produce Planck scale quantities of natural phenomena. For example, impedance has units of volts per amp and the impedance of free space is created using the ratio of Planck’s constant to the elementary charge squared. In Planck units, we see that Z0 is the Planck impedance—the ratio of Planck voltage to Planck current.
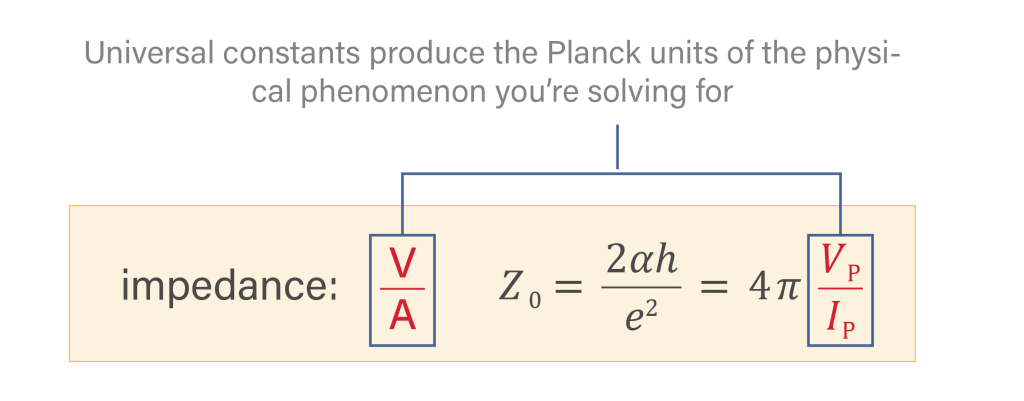
The following arrangements of universal constants produce Planck scale quantities of each phenomenon we wish to solve for. These quantities are conserved as the scale of the phenomenon changes.

Non-dimensional quantities
Students might wonder why non-dimensional quantities of physical phenomena appear repeatedly in the Planck unit equations.

Teachers can make dimensional analysis resonate with students by showing how non-dimensional quantities translate arbitrary unit systems like the International System of Units (SI) into correlated natural units, allowing us to find one quantity from a correlated quantity. The following illlustration explains why this is the case.

Non-dimensional units explain the role of universal constants in the equations—translating arbitrary units like meters and seconds into correlated natural units.
Unit Scales
The following illustration shows the misalignment of natural units based on the alignment of SI units. Since natural phenomena are correlated at the Planck scale, SI units must be converted into non-dimensional quantities which normalize the unit system. This is the role of Planck units which are injected into the equations by universal constants.
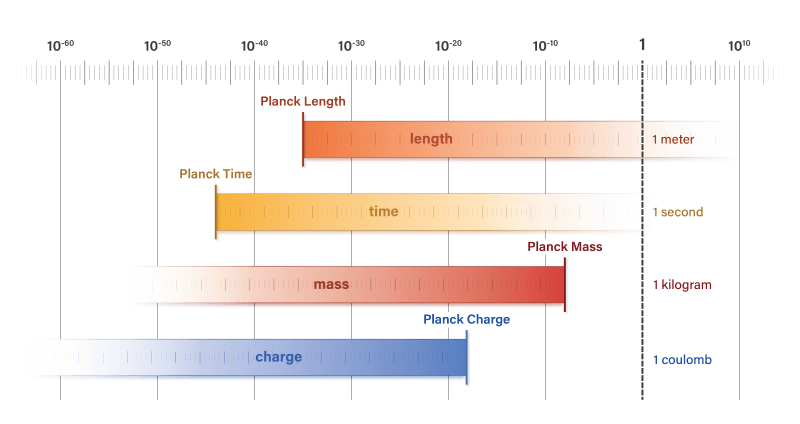
https://doi.org/10.1088/1361-6404/ad61d3. Licensed under CC BY 4.0. Any further distribution must maintain this attribution.
The natural unit system aligns units of length, mass, time, and charge at the Planck scale, where each unit is equal to 1.
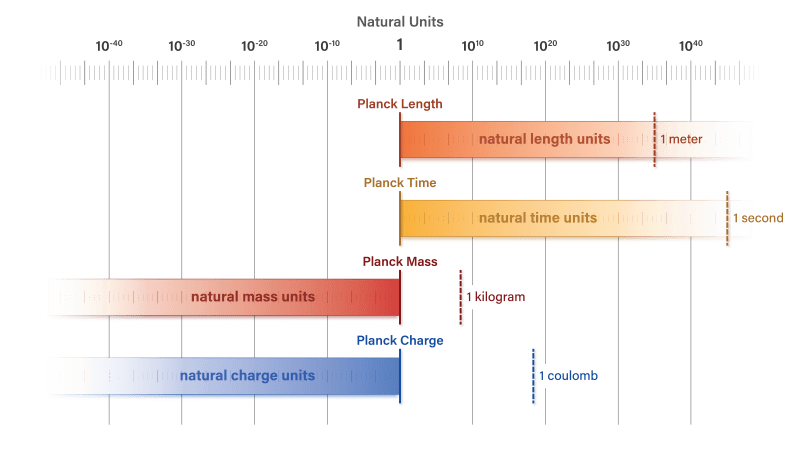
https://doi.org/10.1088/1361-6404/ad61d3. Licensed under CC BY 4.0. Any further distribution must maintain this attribution.