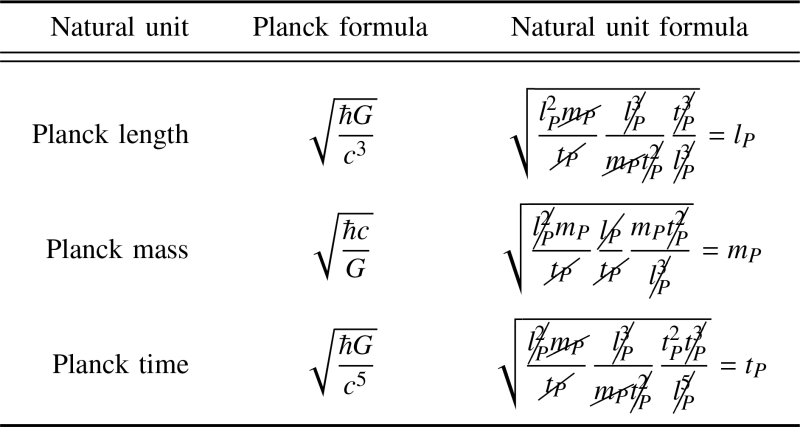
Students are generally taught to perform dimensional analysis by setting universal constants equal to 1 which takes advantage of natural correlations otherwise hidden by arbitrary units. A more insightful way of teaching these correlations is to restate compound-dimensional constants as Planck units in each unit dimension. This gives a more granular form of the equations and correlations.
The 2022 CODATA adjustment of Fundamental Physical Constants published by the US National Institute of Standards and Technologies shows that the speed of light and Planck constant are equal to Planck units in their unit dimensions.

and

Evaluating other universal constants shows that they are similarly equal to Planck units in their unit dimensions.
| Image | Name | Dimensions | File Type | File Type | |
|---|---|---|---|---|---|
 | Speed of light | L T–1 | PNG | PSD | |
 | Planck constant | L2MT–1 | PNG | PSD | |
 | Gravitational constant | L3 M–1 T–2 | PNG | PSD | |
 | Magnetic constant | L M T2 Q–2 T–2 | PNG | PSD | |
 | Electric constant | Q2 T2 L–3 M –1 | PNG | PSD | |
 | Elementary charge | Q | PNG | PSD |
That universal constants comprise natural units was Planck’s assumption when he isolated quantites for each unit dimension from universal constants. Replacing universal constants with Planck units illustrates how the other units cancel out.
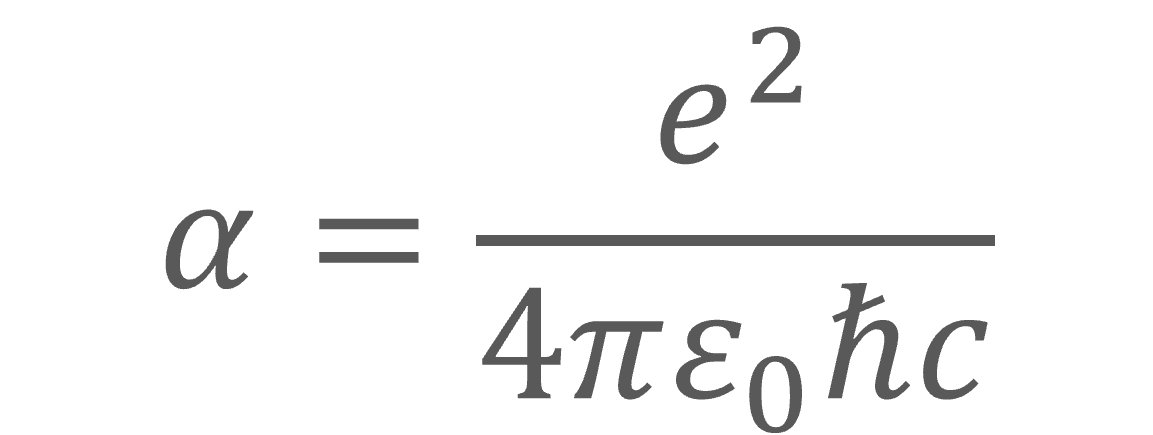
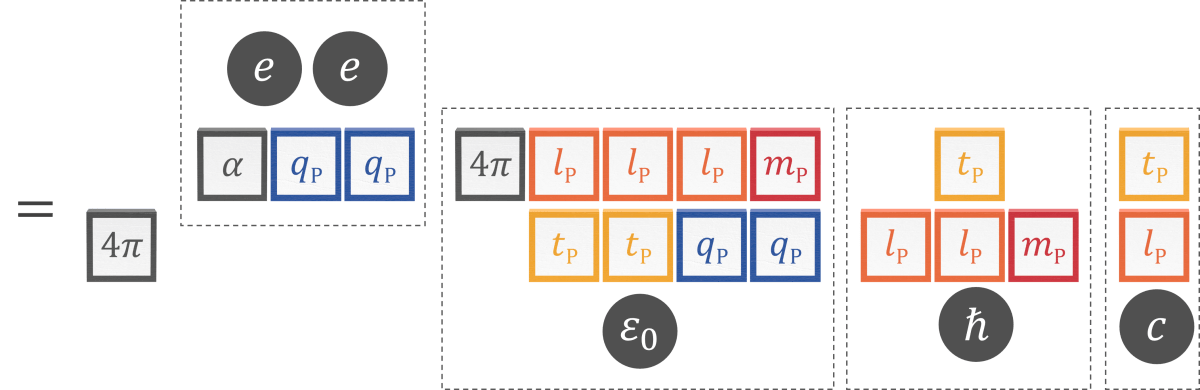
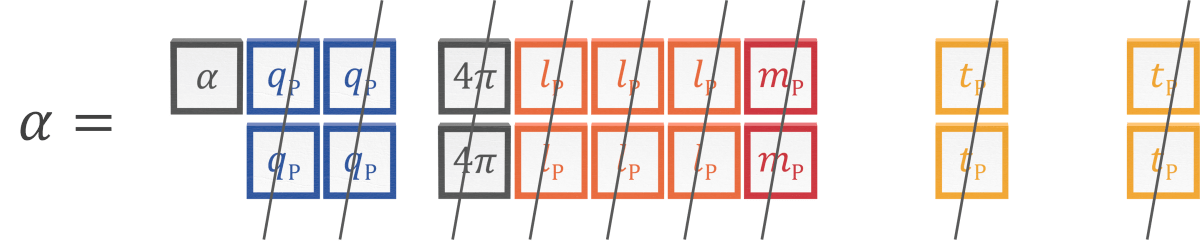
The following blocks are visual representations of natural units of length, mass, time, and charge. Universal constants are collections of single-dimensional Planck units constructed as if assembling blocks into specific arrangements for a particular calculation.
| Image | Name | Dimensions | File Type | File Type | |
|---|---|---|---|---|---|
 | Planck Length | L | PNG | PSD | |
 | Planck Mass | M | PNG | PSD | |
 | Planck Time | T | PNG | PSD | |
 | Planck Charge | Q | PNG | PSD | |
Individual Planck units can be combined into compound-dimensional Planck units. Compound-dimensional units represent Planck scale quantities of physical phenomena and are the basis for calculating observable quantities.
| Image | Name | Dimensions | File Type | File Type | |
|---|---|---|---|---|---|
 | Planck Velocity (Speed of Light) | L T–1 | PNG | PSD | |
 | Planck Acceleration | L T–2 | PNG | PSD | |
 | Planck Force | L M T–2 | PNG | PSD | |
 | Planck Energy | M L2 T–2 | PNG | PSD | |
 | Planck Electric Potential | M L2 T–2 Q–1 | PNG | PSD | |
 | Planck Current | Q T–1 | PNG | PSD | |